Getting started with regressions in STATA
In this guide you will:
- Understand regressions in STATA
- Learn how to code simple and multiple linear regressions
- Interpret regression output (coefficients, p-values, R-squared, and residuals)
- Work with categorical variables
This guide is designed to help you build confidence in reading and interpreting regression results in STATA. Whether you're a beginner or refreshing your understanding, this walkthrough will clarify how to interpret key regression outputs like coefficients, p-values, R-squared, and their residuals, and explain what they tell us about the relationships between variables.
We'll walk through both simple and multiple linear regressions, starting with this data set “ChickWeight” (click here to download), exploring the relationship between chick weight (gm) and time (days), and then moving on to an economic dataset from the wooldridge package. Along the way, you'll learn :
We'll walk through both simple and multiple linear regressions, starting with this data set “ChickWeight” (click here to download), exploring the relationship between chick weight (gm) and time (days), and then moving on to an economic dataset from the wooldridge package. Along the way, you'll learn :
- How to interpret the effects of each predictor variable
- How to interpret control variables
- How to deal with different variable types in STATA
What is a regression?
Regressions are one of the most widely used tools in data analysis. They help us understand how one variable relates to another, and allow us to predict outcomes using known inputs.
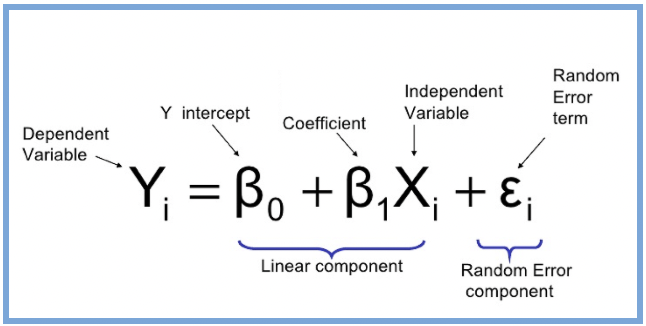
At its core, a regression is a way to model the relationship between:
- One outcome variable (also called the dependent variable or Y)
- And the one or more predictor variables (called the independent variables or X)
In STATA:
The regress command fits a model of dependent variables (depvars) on independent variables (indepvars)
Regress [y variable] [independent variables], [options]
The regress command fits a model of dependent variables (depvars) on independent variables (indepvars)
Regress [y variable] [independent variables], [options]
We will perform a deep dive into each of the above metrics and how to read them, with the goal of understanding what each metric is telling us about the model. To do this we 'll be using a data set that is called “ChickenWeight”. This data set has 578 rows and 4 columns, from an experiment on the effect of diet on early growth of chicks. To start, we will be investigating the relationship between chick weight (gm) and time (days) asking: How does the weight of a chick change over time?
This code allows you to see and understand the data set:
This code allows you to see and understand the data set:
Stata
* Load the dataset from the URL
import delimited "https://calmcode.io/static/data/chickweight.csv", clear
Stata
*View the first few rows
list in 1/10NOTE: The period (.) shown at the start of the command in the picture (before
list in 1/10) is not part of the code you need to write. This period appears at the start of any line of code written in Stata and is just a line delimiter used by Stata to display commands; it’s not something you type yourself. Hence, you should start your command directly with list in 1/10 without the period.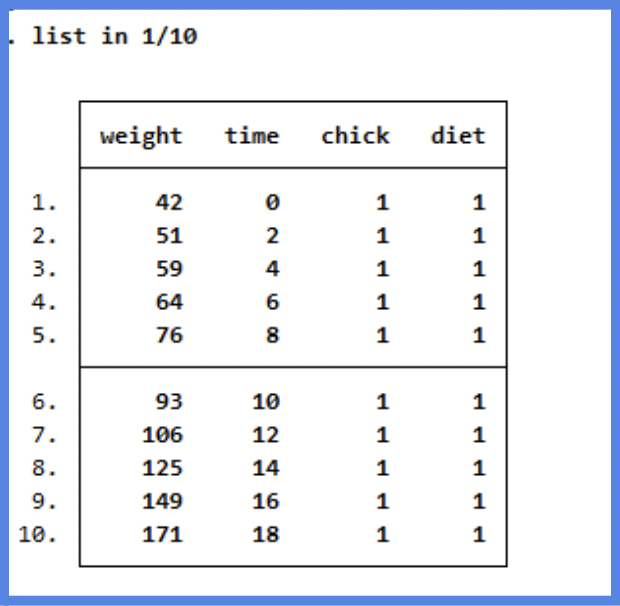
Stata
browse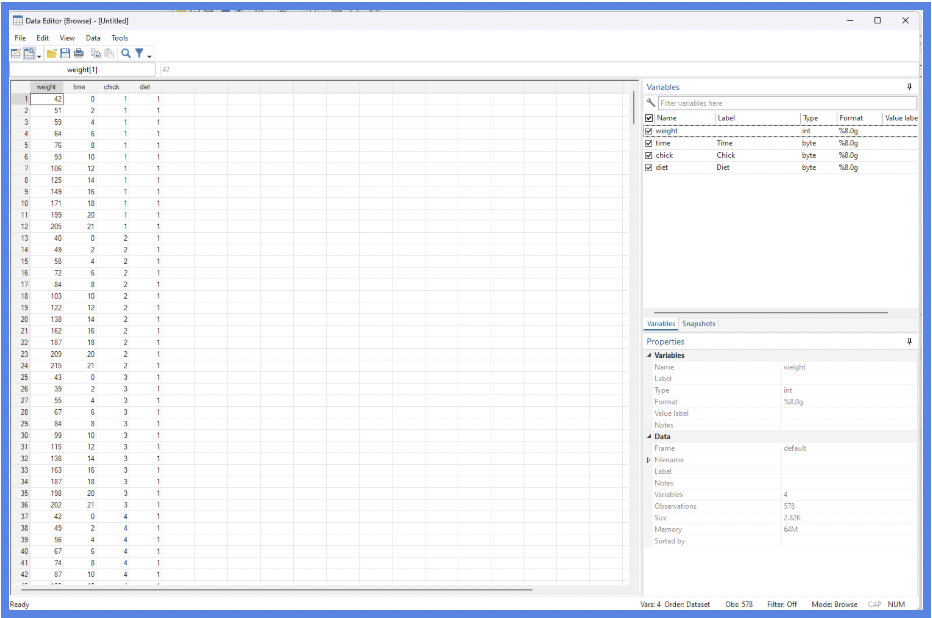
NOTE: The
browse command in Stata lets you view the dataset in a spreadsheet-like window, similar to Excel. You can scroll through all the observations and variables, but by default, the Data Browser is read-only, meaning you can look but not edit. If you want to manually edit the data, you can either use the edit command or simply click the pencil icon at the top of the Stata window to switch the Data Browser into edit mode.
Stata
*View variable names & type
describe weight time chick diet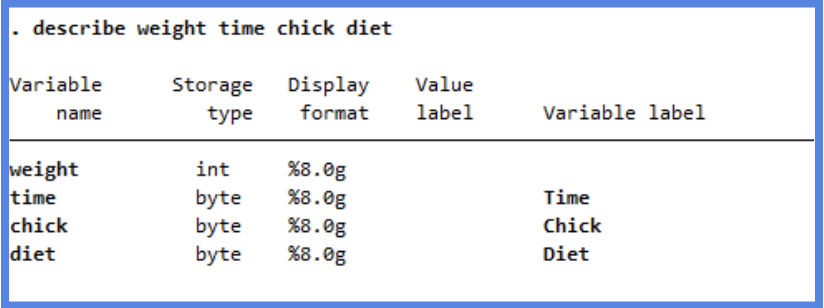
Variables:
- weight: Numeric variable indicating the body weight of each chick in grams. This is a continuous numerical variable.
- Time: Numeric variable indicating the number of days since birth when the weight was measured. This is a discrete numerical variable, typically treated as continuous in analysis.
- Chick: Identifier for each chick, originally coded as an ordered factor in R. In STATA, it functions as a categorical ordinal variable that uniquely identifies each chick and reflects final weight ranking within diet groups.
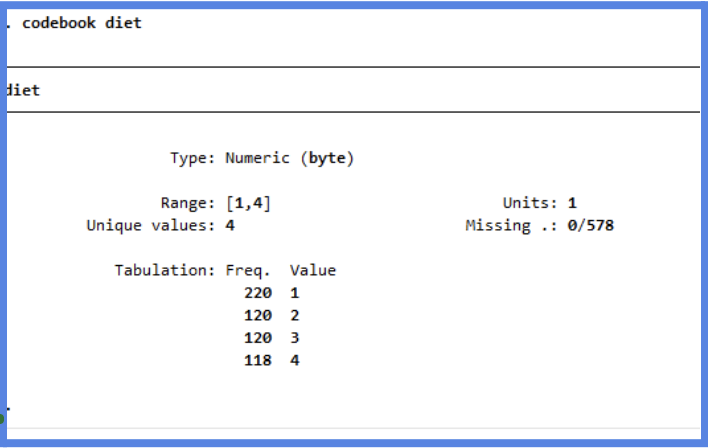
- Diet: Categorical variable indicating the experimental diet assigned to the chick, with values 1 through 4. This is a nominal categorical variable, meaning the numbers are just labels with no inherent order (i.e., diet 2 is not “more” or “less” than diet 1).
Important note on categorical variables:
Categorical variables represent groups, labels, or categories. They can be:
- Nominal: no natural order (e.g., diet groups, colors, brands)
- Ordinal: clear ranking or order (e.g., small, medium, large; satisfaction scores)
- 1 → Diet group 1
- 2 → Diet group 2
- 3 → Diet group 3
- 4 → Diet group 4
Stata
*Summary Statistics
summarize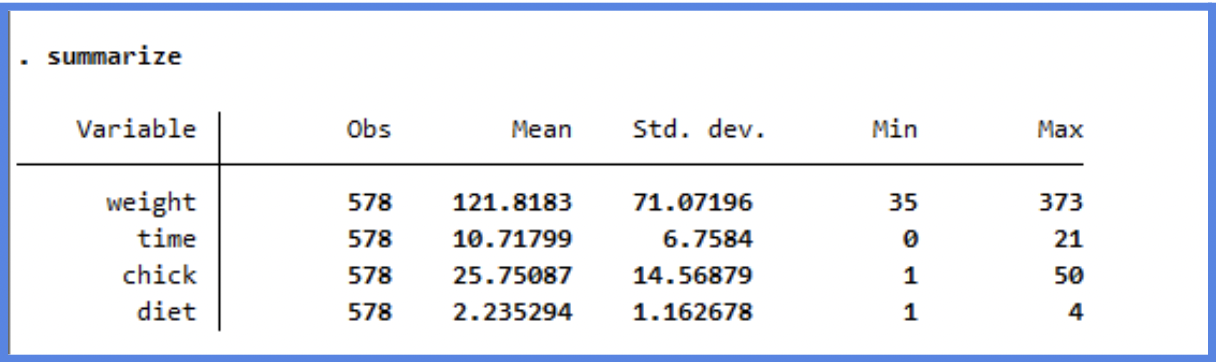
However, it’s important to note that in Stata, when you use commands like summarize, you will get these same statistics for both numerical and categorical variables. This is because Stata treats categorical variables stored as numbers (like diet = 1, 2, 3, 4) just like any other numeric variable. This means you will see a mean and standard deviation even for variables that are actually labels or groups, though these numbers often have no meaningful interpretation.
If you want appropriate summaries for categorical variables, such as counts and percentages, you should use tabulation commands like tabulate diet or codebook diet. These commands give you frequency tables that show how many observations fall into each category, helping you check for balanced groups, unexpected codes, or missing data.
Understanding the difference between numeric and categorical summaries and knowing which commands to use is crucial to avoid misinterpreting your data.
If you want appropriate summaries for categorical variables, such as counts and percentages, you should use tabulation commands like tabulate diet or codebook diet. These commands give you frequency tables that show how many observations fall into each category, helping you check for balanced groups, unexpected codes, or missing data.
Understanding the difference between numeric and categorical summaries and knowing which commands to use is crucial to avoid misinterpreting your data.
How to Run a Simple Linear Regression in STATA
We’ll start by running a simple regression model with time as our dependent variable and chicken weight (gm) as our independent variable. The code and the output of this regression model are below.
Stata
regress weight Time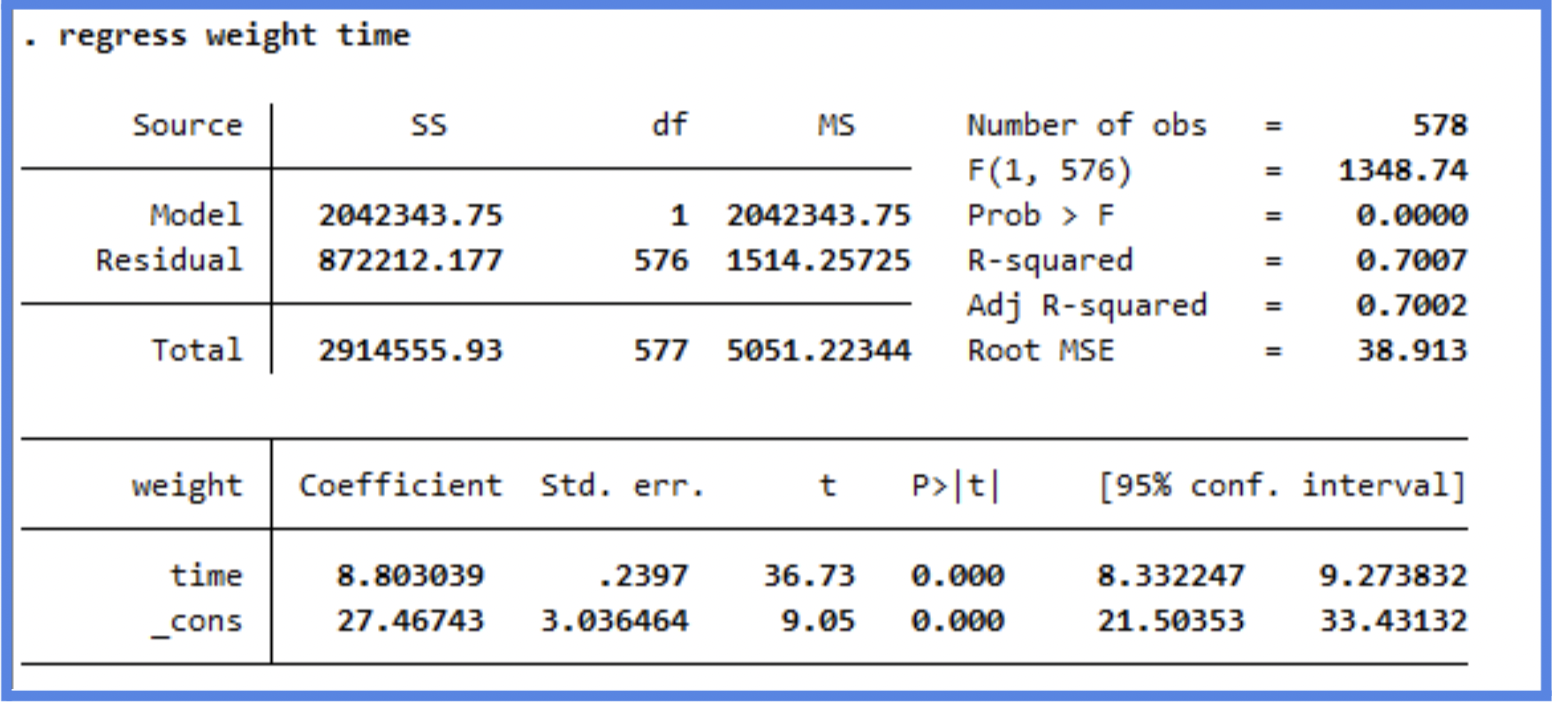
Now that we have a model and output, let's walk through each part of the model step by step so we can better understand each section and how it helps us determine the effectiveness of the model.
Coefficients
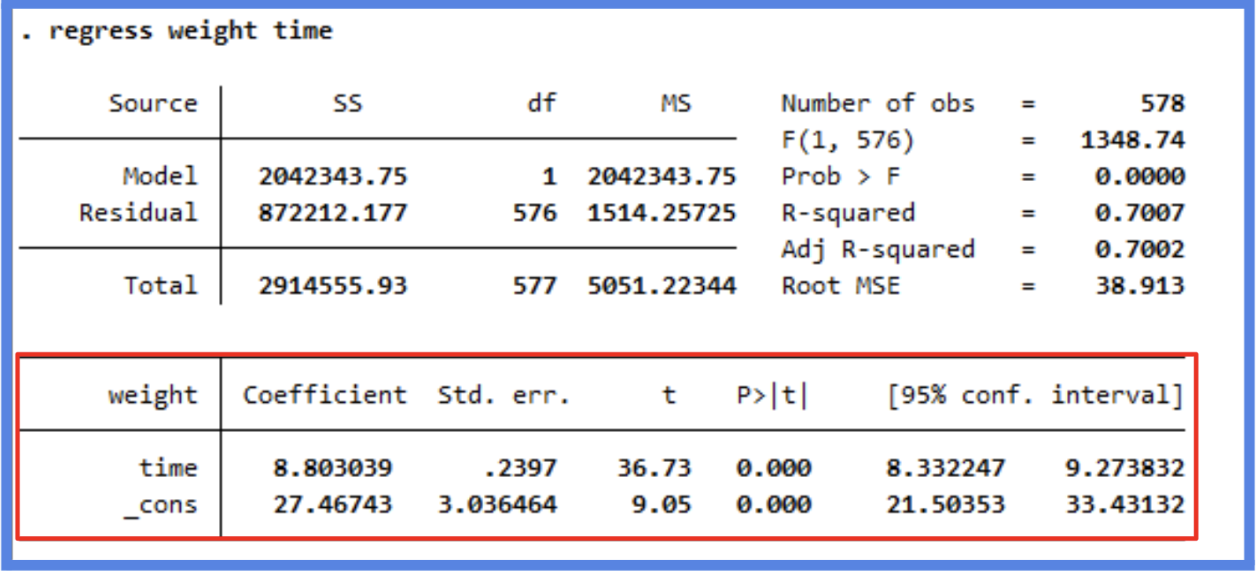
The next section in the model output talks about the coefficients of the model. We are looking to build a generalized model in the form of the slope equation, y=mx+b, where b is the intercept and m is the slope of the line. Because we often don’t have enough information or data to know the exact equation that exists in the wild, we have to build this equation by generating estimates for both the slope and the intercept.
These estimates are most often generated through the ordinary least squares method (OLS), which is a fancy way of saying that the regression model finds the line that fits the points in such a way that it minimizes the distance between each point and the line (minimizes the sum of the squared differences between the actual values and the predicted values).
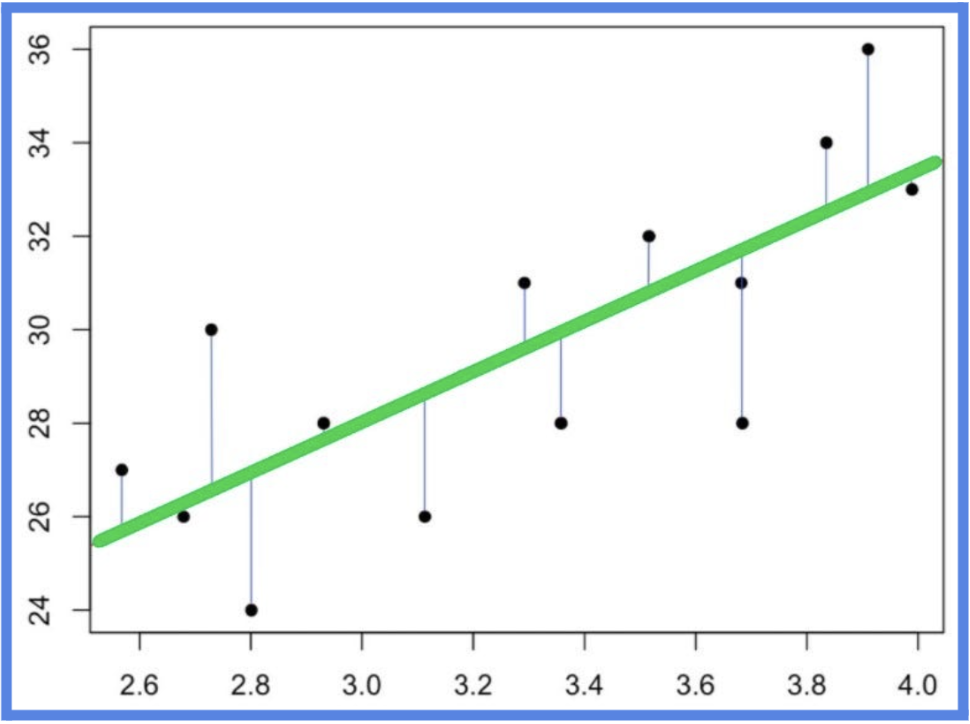
The line above is a visual representation of how we obtain our coefficients. The point at which the line meets the y-axis is our intercept (b) and the slope is our (m). With this we can build our model equation:
Predicted Weight=27.47+8.80×Time
How do we interpret each estimate? The (intercept) can be interpreted as follows: when Time=0, a chick weighs 27.47 grams, in other words, when born (time =0) a chick will weigh 27.47 grams on average.
The Time estimate can be interpreted as follows:On average, for each additional day, a chick gains about 8.80 grams of weight.
The Time estimate can be interpreted as follows:On average, for each additional day, a chick gains about 8.80 grams of weight.
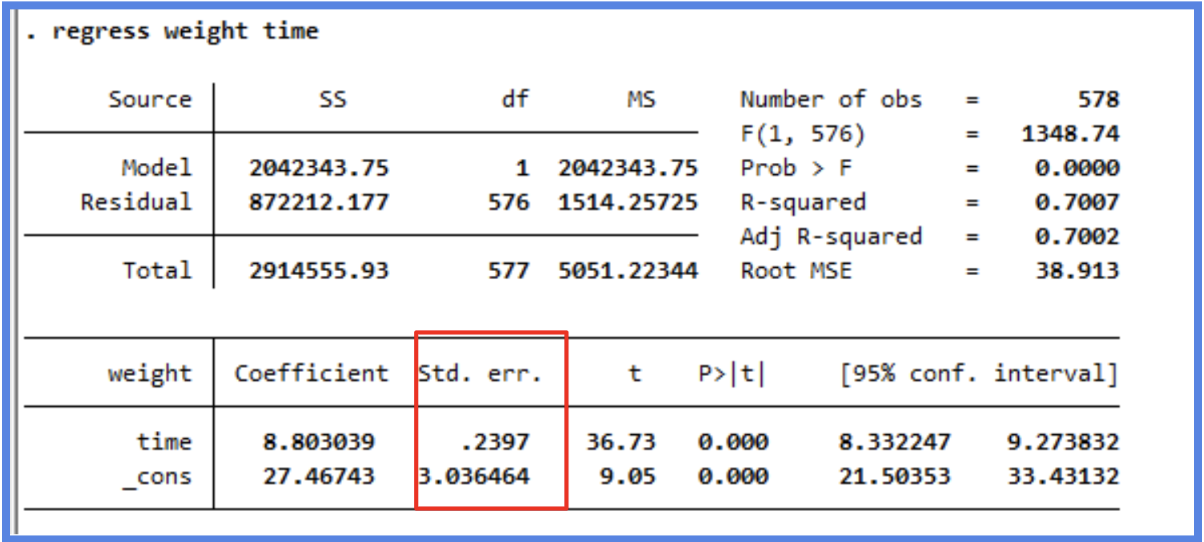
Coefficients – Std. Error
The standard error of the coefficient is an estimate of the standard deviation of the coefficient. In effect, it is telling us how much uncertainty there is with our coefficient. The standard error is often used to create confidence intervals. For example we can make a 95% confidence interval around our slope by multiplying by 1.96, time:
8.8030±1.96(0.2397)=(8.3334, 9.2726)
Looking at the confidence interval, we can say that we are 95% confident the actual slope is between 8.33 and 9.27.
Apart from being helpful for computing confidence intervals and t-values, this is also a quick check for significance. If the coefficient is large in comparison to the standard error, the confidence interval will not include zero—which suggests the coefficient is statistically significant. In our case, since the interval does not include 0, we can confidently say that time has a significant positive effect on chick weight.
Controlling for heteroskedasticity:
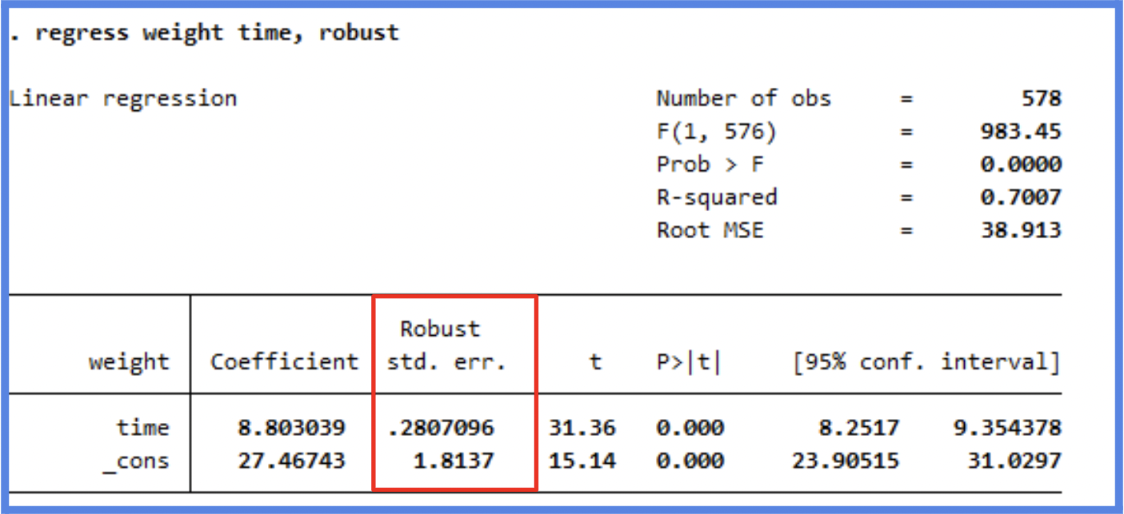
You’ll often see the , robust option added at the end of the regression command (for example, regress csat expense, robust). This tells Stata to calculate robust standard errors that correct for heteroskedasticity — meaning, when the variance of the residuals is not constant across all levels of the independent variable(s). Heteroskedasticity can bias your standard errors and lead to incorrect conclusions about statistical significance.
By using robust standard errors, you protect your inference (like p-values and confidence intervals) from these issues, making your model’s estimates more reliable.
NOTE: The
, robust option does not change the coefficients! It only adjusts the standard errors and related statistics. Even if no heteroskedasticity is present, it’s often considered good practice to report robust standard errors.Robust Regression, controlling for heteroskedasticity
![]()
Normal Regresion without control
![]()
Coefficients – t-value
The t-statistic is simply the coefficient divided by the standard error. In general, we want our coefficients to have large t-statistics, because that indicates the standard error is small relative to the estimate, meaning our estimate is more precise. Simply put, the t-statistic tells us how many standard errors away from zero the coefficient is.
In our example, the coefficient for Time is 36.73 standard errors away from zero, which is extremely far in statistical terms. The larger the t-statistic, the more confident we are that the coefficient is not zero, i.e., that it represents a real effect. The t-statistic is then used to calculate the p-value, which helps us determine the statistical significance of the coefficient.
Coefficients – Pr(>|t|) and significance
In the regression output, the Pr(>|t|) column shows the p-value for each coefficient. This represents the probability of observing a t-statistic as extreme as the one calculated, assuming the null hypothesis is true (i.e., assuming the true coefficient is 0). In simple terms, we ask: “if there is no relationship, what are the chances we'd get a t-value this big?” Small p-values (typically < 0.05) suggest that the observed relationship is unlikely to be due to chance. A small p-value allows us to reject the null hypothesis and conclude that the coefficient likely represents a real effect.
In our model, the p-value for both the intercept and Time is 0.000. Since it is lower than 0.05 we can reject the null. So we can say that the time coefficient is highly significant, confirming a strong relationship between time and weight. Every day, chicks gain approximately 8.80g, and this growth rate is very unlikely to be due to random variation.
R-Squared

The R-squared (R²) statistic provides a measure of how well the model fits the actual data. It represents the proportion of variance in the response variable that is explained by the predictor(s). R² values range from 0 to 1, where:
- A value near 0 means the model explains very little of the variation.
- A value near 1 means the model explains most of the variation.
In our example, the Multiple R-squared is 0.7007. This means that approximately 70% of the variation in chick weight can be explained by the variable Time. That’s a fairly strong relationship, especially considering we’re using only one predictor. Think about it: if you were trying to predict a chick’s weight, wouldn’t age (time) be one of the most important variables? It makes intuitive sense that as chicks get older, they gain weight, so it’s not surprising that Time is a strong predictor.
That said, it’s always important to note that what constitutes a "good" R² depends on the context. In some fields (like biology or economics), even an R² of 0.3 might be meaningful, while in others (like physics), 0.9 might be expected.
NOTE: In multiple regression settings, the “Multiple R-Squared” will always increase as more variables are included in the model. That's why the adjusted R-squared is the preferred meas
F- Statistic
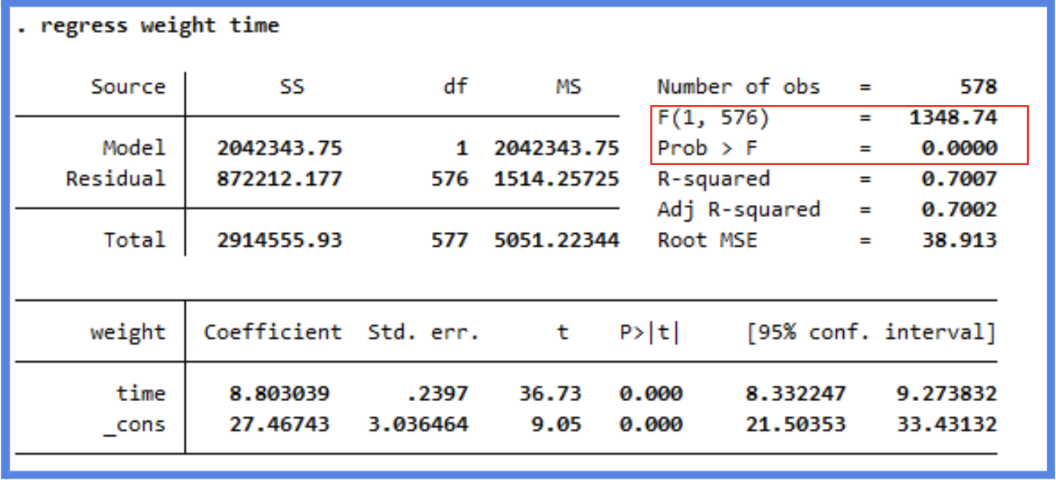
When running a regression model, either simple or multiple, a hypothesis test is being run on the global model. The null hypothesis is that there is no relationship between the dependent variable and the independent variable(s) and the alternative hypothesis is that there is a relationship. Said another way, the null hypothesis is that the coefficients for all of the variables in your model are zero. The alternative hypothesis is that at least one of them is not zero. The F-statistic and overall p-value help us determine the result of this test. Looking at the F-statistic alone can be a little misleading depending on how many variables are in your test. If you have a lot of independent variables, it’s common for an F-statistic to be close to one and to still produce a p-value where we would reject the null hypothesis. However, for smaller models, a larger F-statistic generally indicates that the null hypothesis should be rejected. A better approach is to utilize the p-value that is associated with the F-statistic. Again, in practice, a p-value below 0.05 generally indicates that you have at least one coefficient in your model that isn’t zero.
We can see from our model, the F-statistic is very large and our Prob > F is zero. This would lead us to reject the null hypothesis and conclude that there is strong evidence that a relationship does exist between chick weight and time.
Number of observations and uncertainty:
When interpreting regression results, it’s important to remember that the number of observations (sample size) directly affects the level of uncertainty around your estimates. With a small sample, standard errors tend to be larger because the model has less information to reliably estimate the relationship between variables. This leads to wider confidence intervals and higher p-values, making it harder to detect statistically significant effects.
On the other hand, with a large sample, standard errors tend to shrink, reflecting greater precision in the estimates. But be cautious: in very large datasets, even small or trivial effects can become statistically significant, so it’s important to also consider effect size and practical importance, not just p-values.
We can see from our model, the F-statistic is very large and our Prob > F is zero. This would lead us to reject the null hypothesis and conclude that there is strong evidence that a relationship does exist between chick weight and time.
Number of observations and uncertainty:
When interpreting regression results, it’s important to remember that the number of observations (sample size) directly affects the level of uncertainty around your estimates. With a small sample, standard errors tend to be larger because the model has less information to reliably estimate the relationship between variables. This leads to wider confidence intervals and higher p-values, making it harder to detect statistically significant effects.
On the other hand, with a large sample, standard errors tend to shrink, reflecting greater precision in the estimates. But be cautious: in very large datasets, even small or trivial effects can become statistically significant, so it’s important to also consider effect size and practical importance, not just p-values.
Root Mean Standard Error
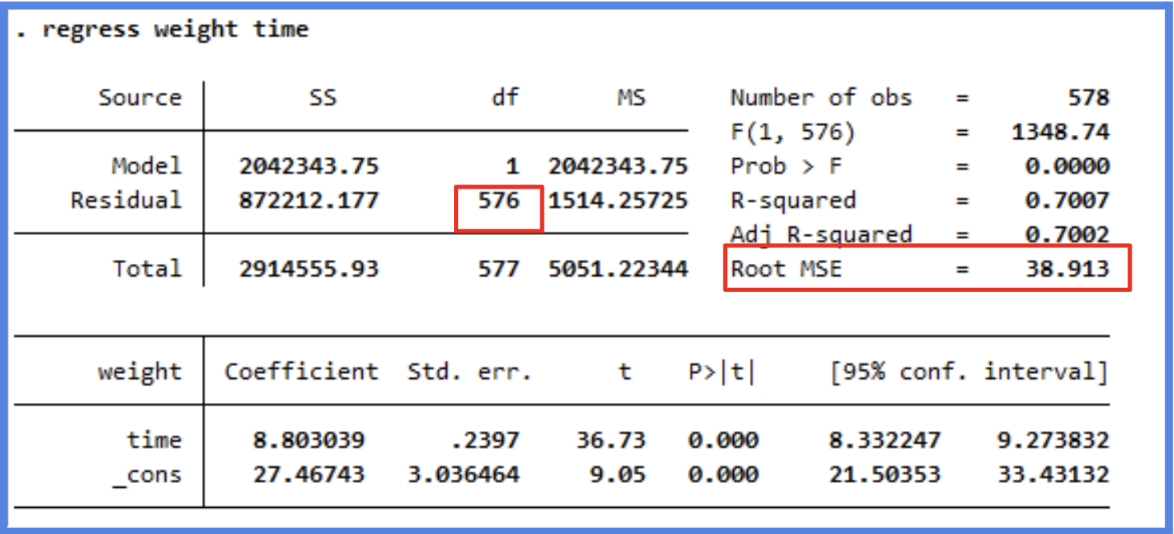
The Root Mean Standard Error is a measure of the quality of a linear regression fit. In theory, every linear model includes an error term (ε), which accounts for the variation in the response variable that is not explained by the predictor(s). Because of this error term, our predictions won’t perfectly match the observed values. The MSE represents the average amount that the observed values deviate from the regression line. In our example, the actual chick weights deviate from the predicted regression line by about 38.91 grams, on average. In other words, even though our model explains a substantial portion of the variation in weight (as shown by the high R²), any individual prediction is still expected to be off by about 38.91 grams on average.
It’s also worth noting that the Residual MSE is calculated with 576 degrees of freedom. Degrees of freedom reflect the number of independent data points used to estimate the model after accounting for the number of parameters estimated (in our case, the intercept and the slope). In our case, we had 578 and two parameters.
NOTE: These statistics are not crucial when reading regression output. Only a limited number of professors or instructors will ask you to interpret this material. However, it’s still interesting and useful to understand, as it can give you additional context about your data and model.
ANOVA Table
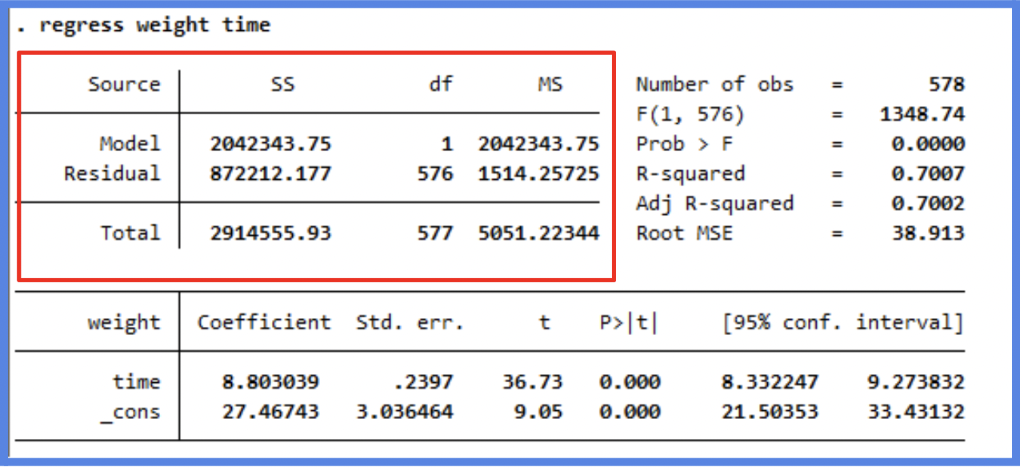
As a final note, it is important to acknowledge the ANOVA table provided at the top of the regression output. This table displays the sum of squares (SS), the degrees of freedom (df) and the mean squares (MS) for both the model and the residuals. These add up to be the total variance in the model. Although not crucial to reading the regression output, these numbers allow us to manually compute the F-statistic and the R-squared. More on this can be explored here.
Adding More Variables to the Regression: Multiple Linear Regression Analysis
Once you've explored a simple linear regression (like predicting weight from time in the ChickWeight dataset), you’re ready to complicate the model by adding more predictors. This is called Multiple Linear Regression. When you include additional variables, these are often referred to as controls, they help you isolate the effect of your main predictor by accounting for other factors that might influence the outcome. In other words, you're holding other variables constant to better understand the unique contribution of each one.
To start, we will continue working with the ChickWeight dataset. In this new model, we’ll include both Time and Diet (categorical with 4 levels) as predictors of weight. Because Diet is categorical, we must include the prefix i. to indicate its factor value.
This is the output we obtain from running the code:
Stata
regress weight time i.diet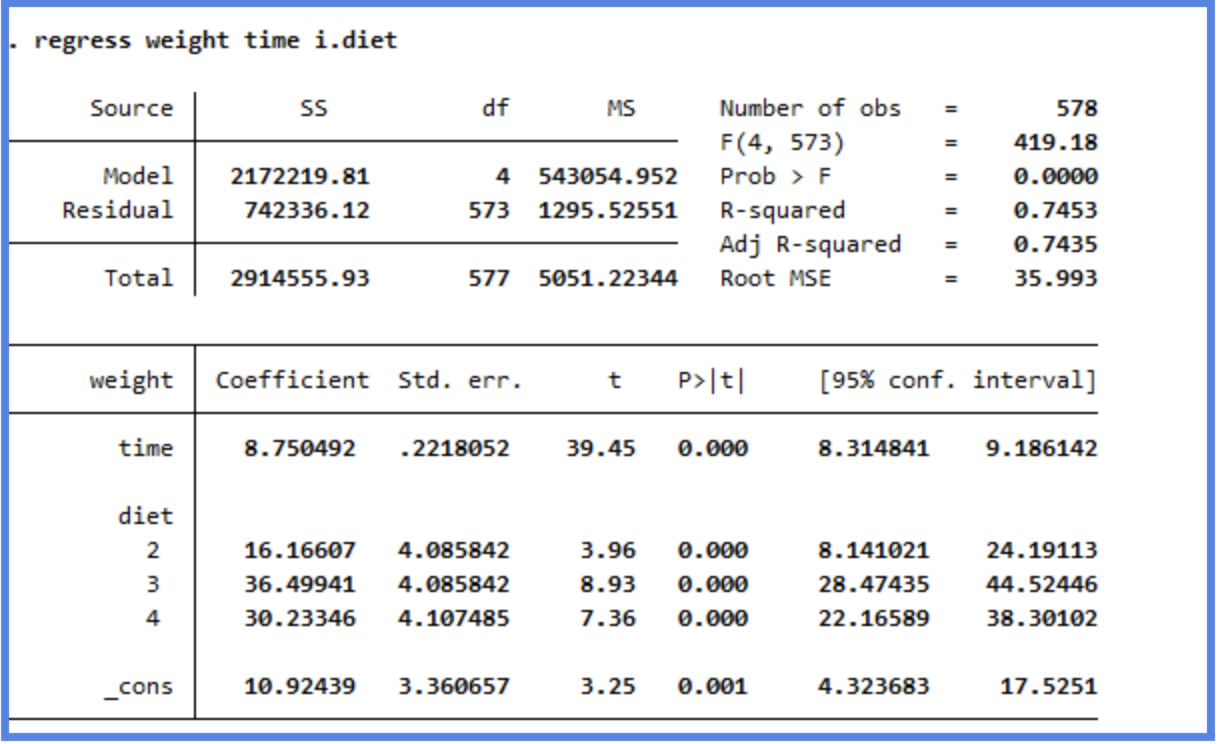
We will interpret the results in the following manner:
- (_cons) Constant(10.92): When Time = 0 (i.e., at birth) and the chick is on Diet 1 (the reference group), the expected weight is 10.92 grams. This is the baseline starting weight.
- NOTE: In regression models, a reference group is the baseline category used when a categorical variable is included in the model. Since regression models can only include numeric values, STATA (and most software) converts categorical variables into dummy variables (binary indicators (0 or 1) for each group). However, one group must be left out to avoid redundancy. This group becomes the reference group. In this case, Diet 1 becomes the reference group, and all other diet coefficients are interpreted in comparison to this reference group.
- Time (8.7505): Holding diet constant, for each additional day since birth, a chick’s weight increases by 8.75 grams. This effect is highly statistically significant (p < 0.001), meaning chicks grow steadily over time.
- Diet Coefficients (relative to Diet 1):
- Diet 2: On average, chicks on Diet 2 weigh 16.17g more than those on Diet 1, controlling for age.
- Diet 3: Chicks on Diet 3 weigh 36.50g more than those on Diet 1.
- Diet 4: Chicks on Diet 4 weigh 30.23g more than those on Diet 1.
All three differences are statistically significant (p < 0.001), indicating that diet type has a clear impact on weight.
Finally, through the R-squared values we can observe that our model explains 74.3% of the variation in chick weight. This is a very strong fit for biological data.
As a result, this multiple linear regression model shows that time since birth and diet type both have strong, statistically significant effects on chick weight. Chicks grow at a steady rate over time, and those on higher-numbered diets, especially Diet 3, tend to weigh more, even after controlling for age.
Economics Data Set
Now we can apply this same logic using a data set from the economics discipline called “bwght” from the Wooldridge package, which explores factors affecting birth weight.
Stata
*Download the package
ssc install bcuse
*Load the data set
bcuse bwghtThe dataset includes 1,388 observations on 14 variables from the 1988 National Health Interview Survey. Below are a few key variables:
| Variable | Meaning | Type |
|---|---|---|
| bwght | Birth weight (ounces) | Continuous numeric |
| famincome | 1988 family income ($1,000s) | Continuous numeric |
| cigs | Cigarettes smoked per day while pregnant | Discrete numeric |
| motheduc | Mother’s years of education | Ordinal numeric |
| white | =1 if white, 0 otherwise | Binary (factor/logical) |
Building a More Complex Linear Model:
Let’s build a multiple linear regression model to predict the impact of smoking cigarettes during pregnancy on infant birth weight (bwght), while controlling for other relevant factors.
This allows us to isolate the effect of smoking from other variables that might also influence birth outcomes, such as mother’s education, income, or race.
Stata
regress bwght cigs motheduc white faminc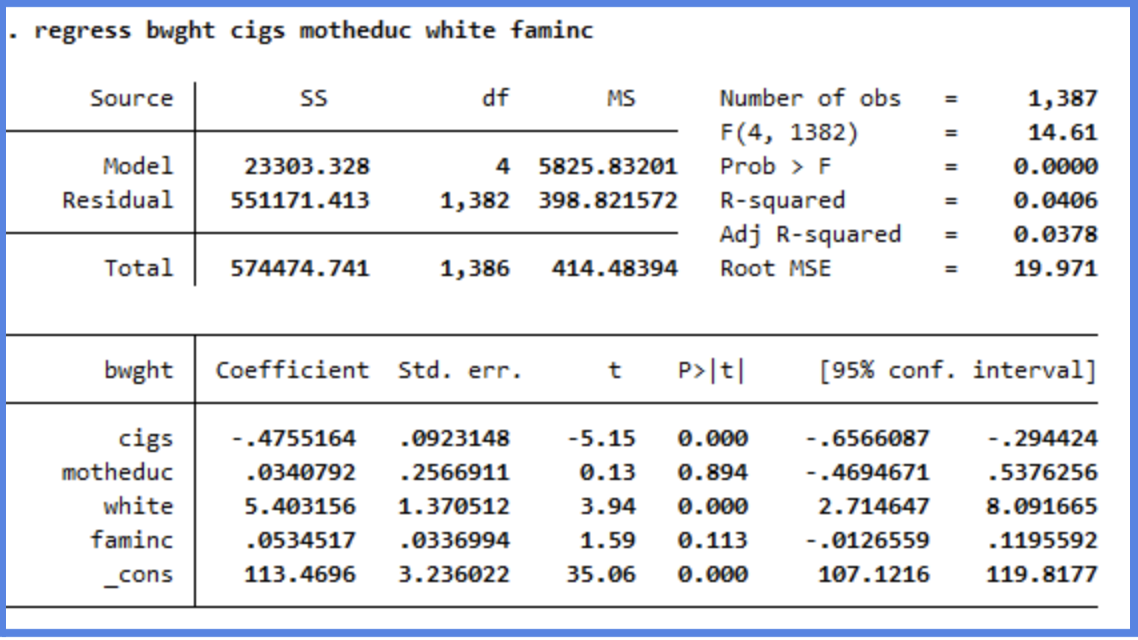
Once again, we will interpret the variables and understand the constants by examining both the magnitude and direction of each coefficient, while keeping in mind the effect of controlling for other variables in the model.
| Variable | Type | Coefficient | Interpretation | Statistical Significance |
|---|---|---|---|---|
cigs |
Continuous |
−0.476 |
When controlling for a mother’s education, race, and income, each additional cigarette smoked per day is associated with a 0.48 oz decrease in birth weight. |
*** (p < 0.001) |
motheduc |
Continuous |
+0.034 |
When controlling for smoking, race, and income, each additional year of mother’s education is associated with a 0.03 oz increase in birth weight. |
Not significant (p = 0.894) |
white |
Binary (Binary variables compare the presence vs. absence of a characteristic, e.g., white vs. other race.) |
+5.403 |
When controlling for smoking, education, and income, being white is associated with a 5.4 oz increase in expected birth weight. |
*** (p < 0.001) |
faminc |
Continuous |
+0.053 |
When controlling for smoking, education, and race, each additional $1,000 in family income is associated with a 0.05 oz increase in birth weight. |
Not significant (p = 0.113) |
Through this, we can observe that the biggest impacts on weight came from being white and smoking cigarettes, but while one decreased the weight by almost 0.5 ounces per cigarette the other one increased the weight by 5.40 pounds just because of race. Both of these effects are statistically significant (p < 0.001), suggesting they likely reflect real relationships rather than random variation. This underscores how certain social and behavioral factors can meaningfully relate to the dependent variable—in this case, infant weight.
It’s also important to note that this model can be expanded to include additional relevant predictors in order to improve its explanatory power (as measured by the R-squared) and to capture more of the variation in the data. For example, we might consider including father’s education, a more detailed measure of smoking such as packs per day, or even factors like maternal age, prenatal care visits, or diet during pregnancy.
It’s also important to note that this model can be expanded to include additional relevant predictors in order to improve its explanatory power (as measured by the R-squared) and to capture more of the variation in the data. For example, we might consider including father’s education, a more detailed measure of smoking such as packs per day, or even factors like maternal age, prenatal care visits, or diet during pregnancy.
CAVEAT: While adding more variables can enhance the model, it also comes with trade-offs. Including too many predictors, especially those that are irrelevant or highly correlated with others, can lead to overfitting, where the model captures noise rather than true patterns. This can reduce its accuracy when applied to new data. Additionally, a more complex model can become harder to interpret and communicate clearly. As mentioned before, it is important to always keep tabs on the adjusted R-squared for this analysis, as it may not increase even when more variables are added.
Thoughtful model expansion allows us to uncover more accurate and nuanced insights into the factors influencing birth weight.
By: Sofia Covarrubias
By: Sofia Covarrubias